Research

Research interests

  • Multi-dimensional compressible hydrodynamics and related systems, bicharacteristics, ...

  • Structure preserving numerical methods, i.e. methods which preserve discrete vorticity, discrete involutions, discrete stationary states, ...

  • Truly multi-dimensional methods

  • (Stabilized) Finite Element methods, Active Flux, ...

  • Low Mach number compliant numerical methods

  • Unstructured grids


    • Active Flux

    The Active Flux scheme is a recent extension of the finite volume scheme. It uses additional pointwise degrees of freedom, continuous reconstructions and is third order accurate. You can find more details here:

    Barsukow, Hohm, Klingenberg, Roe 2018,
    Eymann, Roe 2011,
    van Leer 1977

    If you are interested to try out the Active Flux scheme you can find here a tiny code that implements Active Flux for linear advection in 1d: miniActiveFlux (bitbucket.org).

    Some snapshots (produced with the above minimal code):



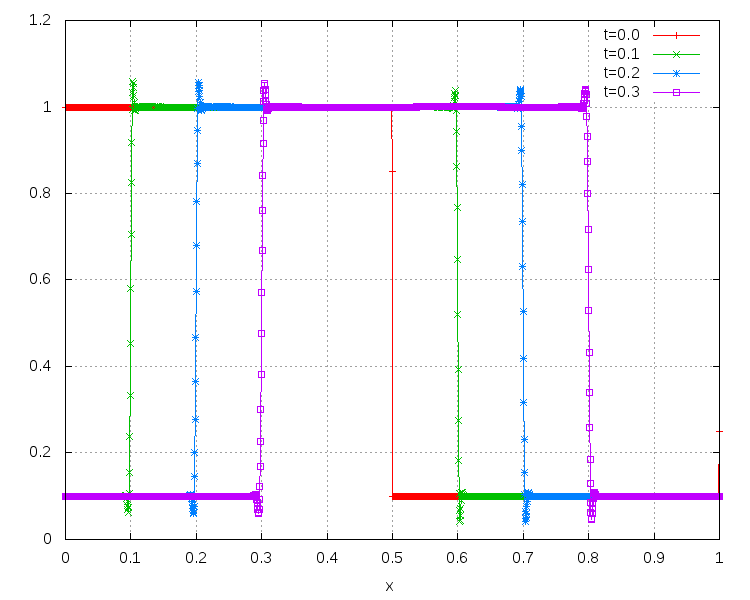
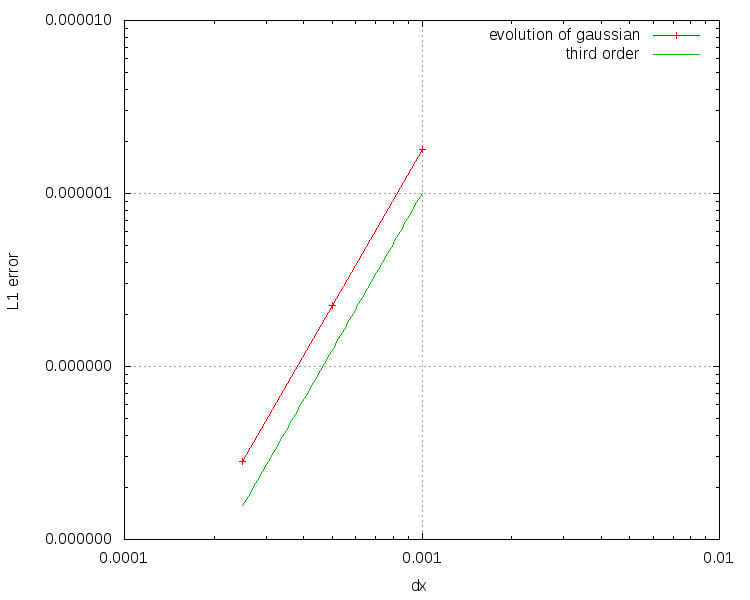
    More sophisticated implementations allow to compute following examples:

    Shallow water equations with wetting and drying



    Kelvin-Helmholtz instability



    Delaunay-like multi-d Riemann Problems for isentropic Euler (see the Art and Science section for more background)




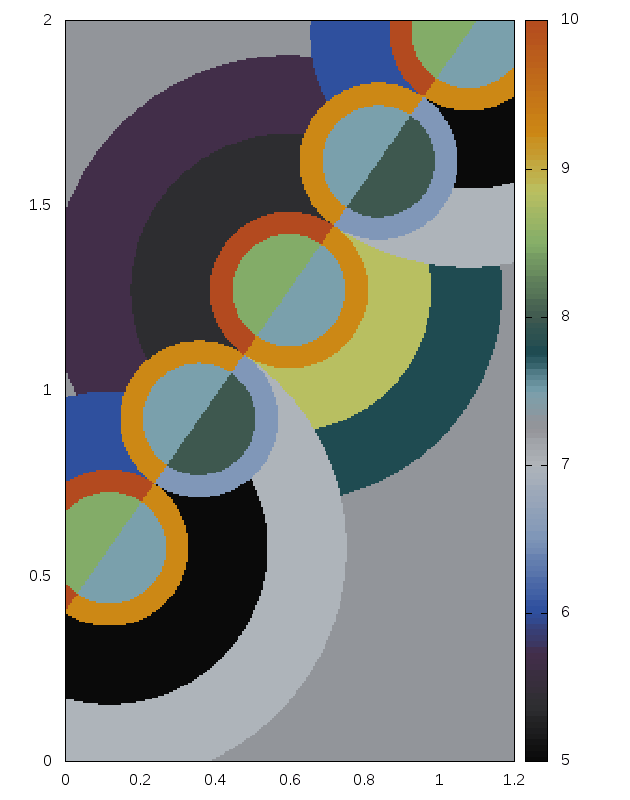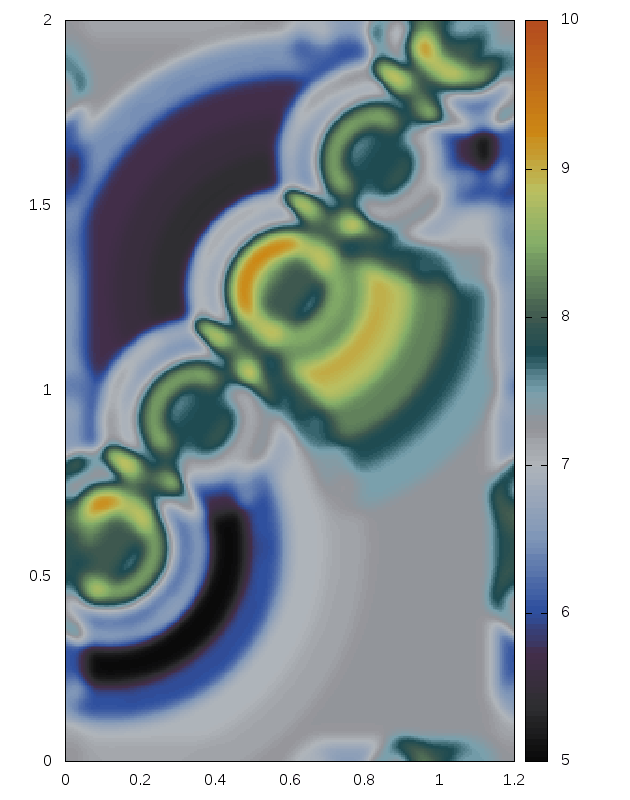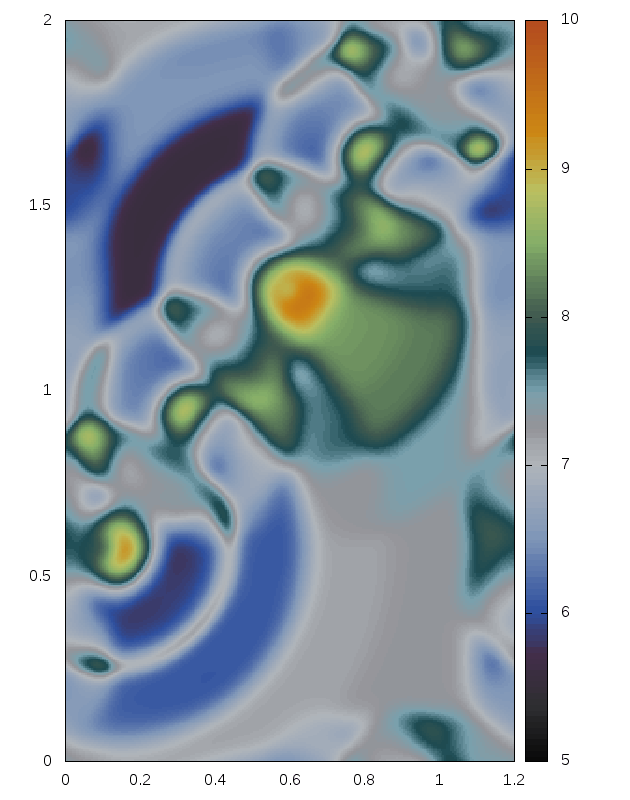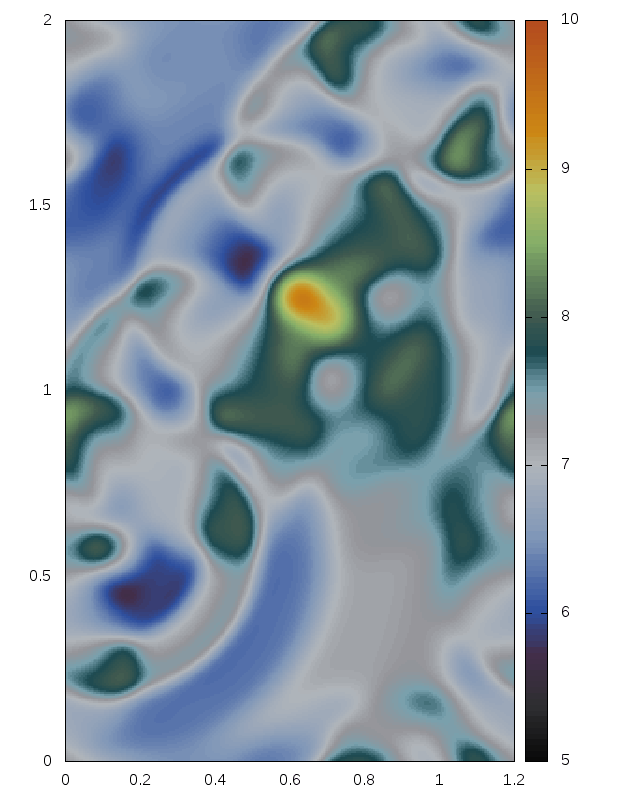
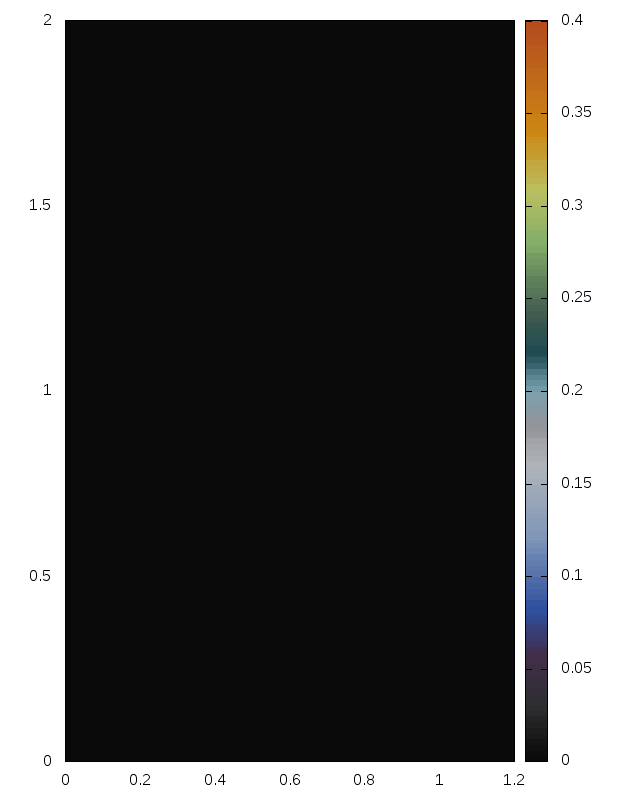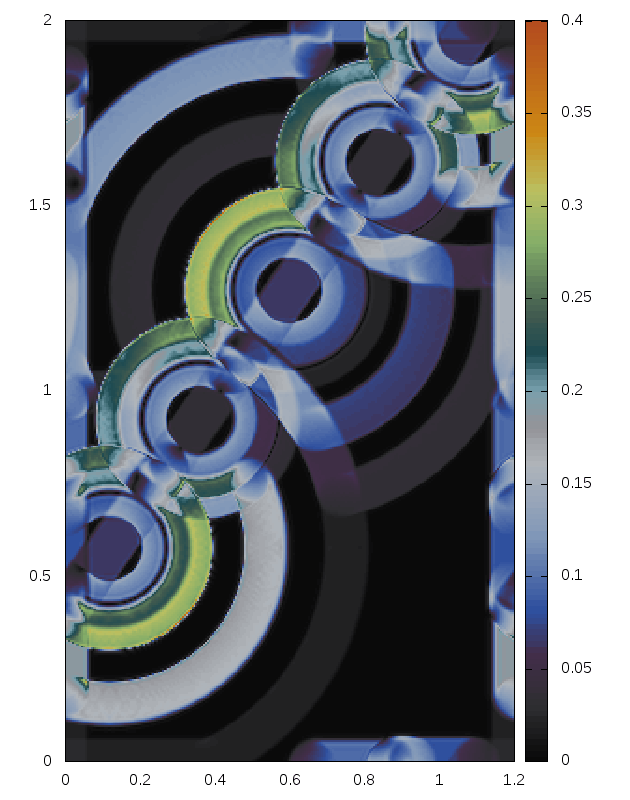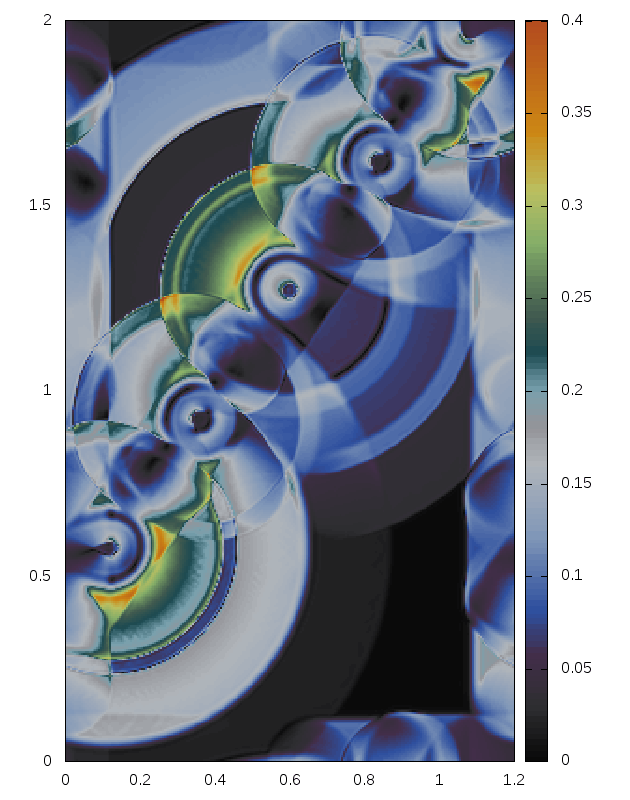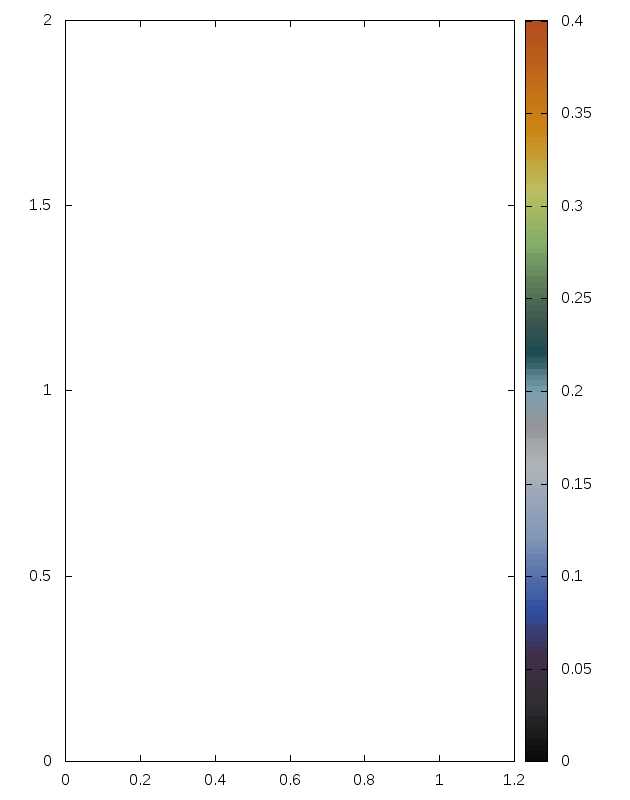
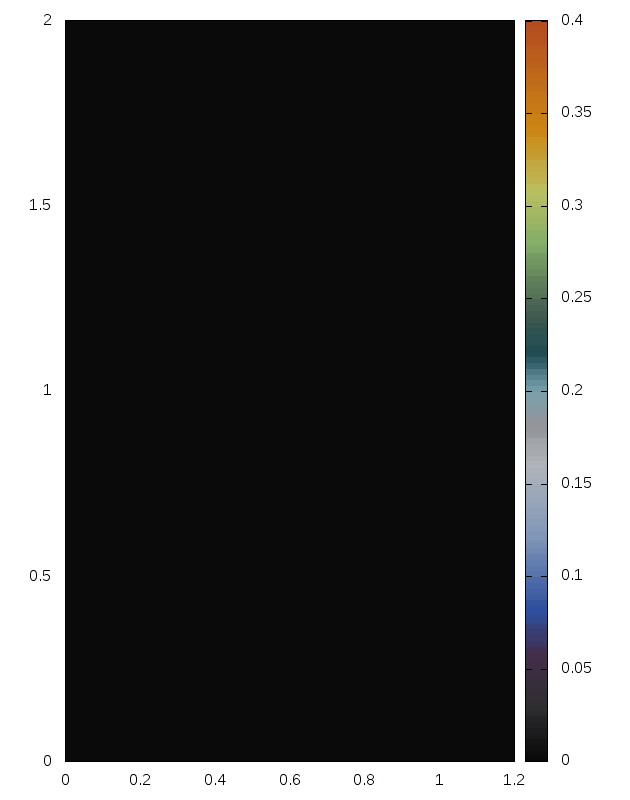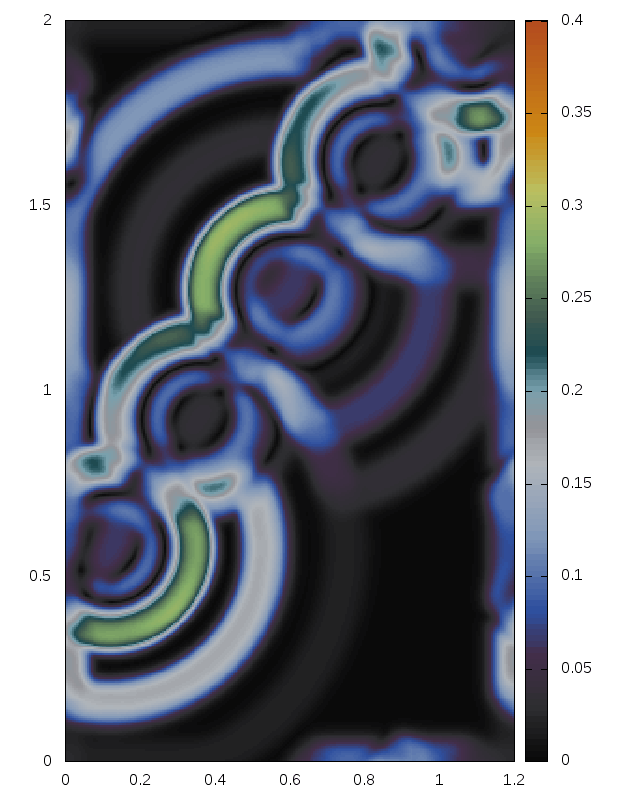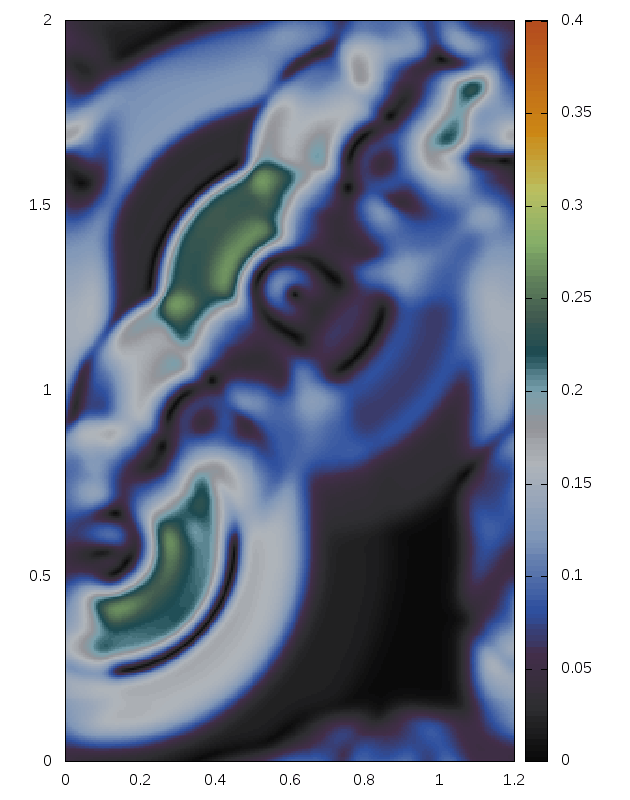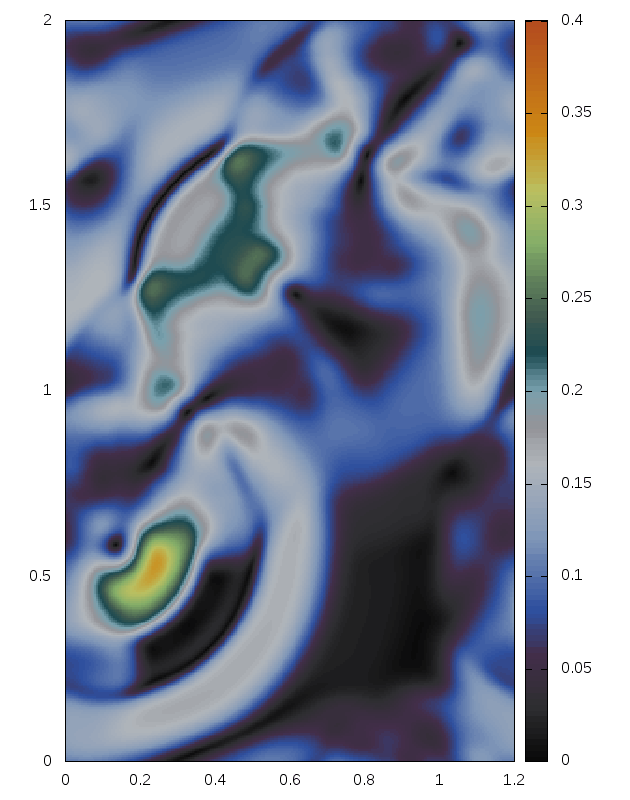
    Right: For comparison results with Roe 1981.



    Linear stability

    For systems or high order methods, linear (von Neumann) stability analysis requires to check whether the eigenvalues of some complex-valued matrix are located inside the unit disc. It is unnecessary (and often very complicated) to compute these eigenvalues. There exist necessary and sufficient conditions for this (discovered by Schur in 1917/18) which do not involve computing the eigenvalues. The starting point is the characteristic polynomial of the matrix.

    I have here some slides discussing the proof (following Miller 1971). In principle, you can perform the analysis analytically, but if your matrix/polynomial depends on parameters, the stability region in the parameter space might turn out to be very complicated. For this case, here is a tiny code (in Java) that implements the algorithm and allows for parameter studies. The important function is boolean isNeumann in class Miller.

    Last modified: Sat Mar 20 18:47:31 CET 2021