of Lake Geneva Sediments
with S+SpatialStats
Reinhard Furrer, Marc G. Genton
Abstract
This paper discusses the use of robust geostatistical methods on a multivariate data set of sediments in the Lake Geneva in Switzerland. Each variable is detrended via non-parametric estimation penalized with a smoothing parameter. The optimal trend is computed with a smoothing parameter based on cross-validation. Then, variograms are estimated by a highly robust estimator of scale. The parametric variogram models are fitted by generalized least squares, thus taking account of the variance-covariance structure of the variogram estimates. Comparison of kriging with or without detrending the data is completed. All these computations are done with the software S+SpatialStats, extended with new functions in S+ that are available via ftp.
Keywords: Robustness; Trend; Variogram; Generalized least squares; Kriging.
Excerpt
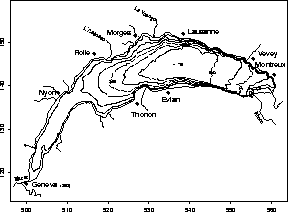
Figure 1: Map of the area of Lake Geneva in Switzerland. The main cities and rivers are represented, as well as the contour lines of the depth of the lake. The Rhone (main river) enters in the east part of the lake and leaves in the west part.
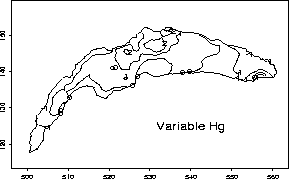
Figure 2: Kriging map for the centred reduced variable Hg. Kriging prediction are calculated over a 100*100 grid inside the lake boundaries.
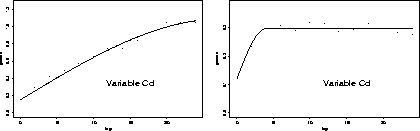
Figure 3: Empirical and fitted variograms of the variable Cd on centered reduced data (left side) and on data with removed trend (right side).
S-Plus functions
Download of the functions for highly robust variogram estimation and generalized least squares fitting. This software may be used, copied and modified freely for scientific and/or non-commercial purposes, provided reference is made. 
Highly robust variogram estimation: |
READ.ME variogram.qn.tar |
|
Generalized least squares fitting: |
READ.ME glse.fitting.tar |
The authors decline any responsibility of the correctness of the functions and any damages that may occur by using them.
The authors appriciate all comments on the functions.
References
Rousseeuw, P.J. and Croux, C. (1993): "Alternatives to the Median Absolute Deviation", Journal of the American Statistical Association, Vol. 88, 1273-1283.Genton, M. G., (1998): "Highly Robust Variogram Estimation", Mathematical Geology, Vol. 30, No. 2, 213-221.
Genton, M. G., (1998): "Variogram Fitting by Generalized Least Squares Using an Explicit Formula for the Covariance Structure", Mathematical Geology, Vol. 30, No. 4, 323-345.
Genton, M. G., (1998): "Spatial Breakdown Point of Variogram Estimators", Mathematical Geology, Vol. 30, No. 7, 853-871.
Furrer, R. and Genton, M. G. (1998): "Robust Spatial Data Analysis of Lake Geneva Sediments with S+SpatialStats", Systems Research and Information Science, Special Issue on Spatial Data: Neural Nets/Statistics, Vol. 8, No. 4, 257-272.